Blog Details

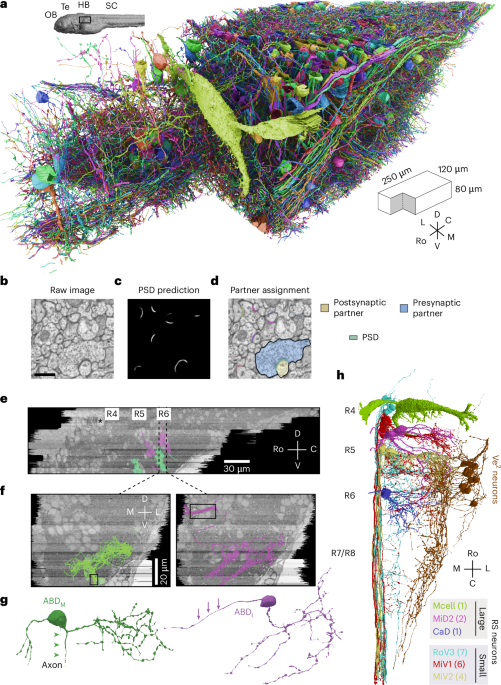
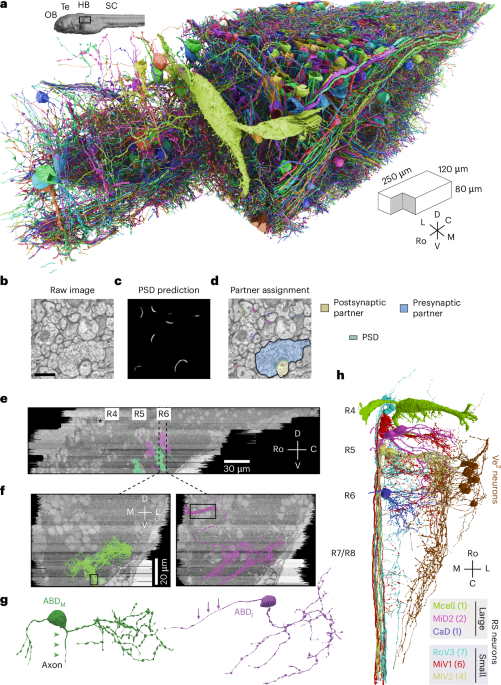
Image acquisition and alignment

We acquired a dataset of the larval zebrafish hindbrain (mitfa^b692/+ (ABxWIK), 6 days after fertilization, sex unspecified, Zebrafish International Resource Center) that extends 250 μm rostrocaudally and includes R4 to R7/R8. The volume extends 120 μm laterally from the midline and 80 μm ventrally from the plane of the Mauthner cell axon. The serial-section Electron Microscopy dataset was an extension of the original dataset in Vishwanathan et al.²² and was extended by additional imaging of the same serial sections. The images were acquired using a Zeiss Field-Emission Scanning Electron Microscope using WaferMapper software⁶⁵. Only a few tens of neurons had been manually reconstructed in our original publication on the ssEM dataset in Vishwanathan et al.²². The dataset was stitched and aligned using the custom package Alembic (see Code availability). The tiles from each section were first montaged in two dimensions (two steps) and then registered and aligned in 3D as whole sections (four steps). Point correspondences for alignment were generated by block matching via normalized cross-correlations both between tiles and across sections. Errors in each step were found by a combination of programmed flags (such as lower than expected correspondences, small search radius, large distribution of norms or high residuals after mesh relaxation) and visual inspection. They were corrected by either changing the parameters or by manual filtering of points. In most cases, the template and the source were both passed through a bandpass filter. The final parameters that were used are listed in Table 1.

Stitching of tiles (montaging) within a single section was split into a linear translation step (premontage) and a nonlinear elastic step (elastic montage). In the premontage step, individual tiles were assembled to have 10% overlap between neighboring tiles, as specified during imaging and by fixing a single tile (anchoring) in place. They were then translated row by row and column by column according to the signal correspondence found between the overlaps. In the elastic montage step, the locations of the tiles were initialized from the translated locations found previously, and blockmatches were computed every 100 pixels on a regular triangular mesh (see Table 1 for the parameters used). Once the correspondences were found, outliers were filtered by checking the spatial distribution of the cross-correlogram (σ filter), height of the peak of the correlogram (Pearson r value), dynamic range of the source patch contrast, kurtosis of the source patch, local consensus (average of immediate neighbors) and global consensus (inside the section). After the errors had been corrected by filtering bad matches, the tiles were modeled as individual spring meshes attached via the matches⁶⁶, and the linear system was solved using conjugate gradient descent. The mean residual errors were in the range of 0.5–1.0 pixels after relaxation.

The intersection alignment was split into a translation step (pre-prealignment), a regularized affine step (prealignment), a fast coarse elastic step (rough alignment) and a slow fine elastic step (fine alignment). In the pre-prealignment step, a central patch of the given montaged section was matched to the previous montaged section to obtain the rough translation between two montaged sections. In the prealignment step, the montaged images were offset by that translation, and then a small number of correspondences were found between the two montaged sections. The sections were then aligned using an affine transformation fit using least squares, regularized with a 10% (empirically derived) weighting of the identity transformation to reduce shear accumulating and propagating across multiple sections. Proceeding sequentially allowed the entire stack to get roughly in place. The mean residual errors after prealignment were in the range of 3.5 pixels after relaxation. In the subsequent rough and fine alignment steps, the blockmatches were computed and filtered between bandpassed neighboring sections in a regular triangular mesh, similar to the elastic montaging step, followed by a conjugate gradient descent on the linear system. Splitting the elastic step into rough and fine alignments allowed the search radius to be reduced during the fine alignment relative to what would have been necessary with a direct attempt, thereby lowering the likelihood of spurious matches as well as the computing time.

Convolutional net training

Dataset

Four expert brain image analysts (D. Visser, Princeton Neuroscience Institute; K.W.; M. Moore, Princeton Neuroscience Institute; and S.K.) manually segmented neuronal cell boundaries from six subvolumes of EM images with the manual annotation tool VAST⁶⁷, labeling 194.4 million voxels in total. These labeled subvolumes were used as the ground truth for training convolutional networks to detect neuronal boundaries. We used 187.7 million voxels for training and reserved 6.7 million voxels for validation.

Network architecture

To detect neuronal boundaries, we used a multiscale 3D convolutional network architecture similar to the boundary detector in Zung et al.⁶⁸. This architecture was similar to U-Net⁶⁹ but with more pathways between scales. We augmented the original architecture of Zung et al.⁶⁸ with two modifications. First, we added a ‘lateral’ convolution between every pair of horizontally adjacent layers (that is, between feature maps at the same scale). Second, we used batch normalization⁷⁰ at every layer (except for the output layer). These two architectural modifications were found to improve boundary detection accuracy and stabilize/speed-up training, respectively. For more details, we refer the reader to Zung et al.⁶⁸.

Training procedures

We implemented the training and inference of our boundary detectors with the Caffe deep learning framework⁷¹. We trained the networks on a single Titan X Pascal GPU. We optimized the binary cross-entropy loss with the Adam optimizer⁷² initialized with α = 0.001, β₁ = 0.9, β₂ = 0.999 and ε = 0.01. The step size α was halved when the validation loss plateaued after 135,000, 145,000 and 175,000 iterations. We used a single training example (minibatch of size 1) to compute gradients for each training iteration. The gradient for target affinities (the degree to which image pixels are grouped together) in each training example was reweighted dynamically to compensate for the high imbalance between target classes (that is, low and high affinities). Specifically, we weighted each affinity inversely proportional to the class frequency, which was computed independently within each of the three affinity maps (x, y and z) and dynamically in each training example. We augmented training data using (1) random flips and rotations by 90°, (2) brightness and contrast augmentation, (3) random warping by combining five types of linear transformation (continuous rotation, shear, twist, scale and perspective stretch) and (4) misalignment augmentation⁷³ with a maximum displacement of 20 pixels in the x and y dimensions. The training was terminated after 1 million iterations, which took about 2 weeks. We chose the model with the lowest validation loss at 550,000 iterations.

Convolutional net inference

The above trained network was used to produce an affinity map of the whole dataset using the ChunkFlow.jl package⁷⁴. Briefly, the computational tasks were defined in a JSON formatted string and submitted to a queue in Amazon Web Services Simple Queue Service (AWS SQS). We launched 13 computational workers locally with NVIDIA Titan X GPU. The workers fetched tasks from the AWS SQS queue and performed the computation. The workers first cut out a chunk of the image volume using BigArrays.jl and decomposed it into overlapping patches. The patches were fed into the convolutional network model to perform inference in PyTorch⁷⁵. The output affinity map patches were blended in a buffer chunk. The output chunk was cropped around the margin to reduce boundary effects. The final affinity map chunk, which is aligned with block size in cloud storage, was uploaded using BigArrays.jl. Both image and affinity map volumes were stored in Neuroglancer precomputed format (https://neurodata.io/help/precomputed/). The inference took about 17 days in total and produced about 26 TB of affinity map.

Chunk-wise segmentation

To perform segmentation of the entire volume, we divided the volume into ‘chunks’. Overlapping affinity map chunks were cut out using BigArrays.jl, and a size-dependent watershed algorithm⁷⁶ was applied to agglomerate neighboring voxels to make supervoxels. The agglomerated supervoxels are represented as a graph where the supervoxels are nodes and the mean affinity values between contacting supervoxels are the edge weights. A minimum spanning tree was constructed from the graph by recursively merging the highest weight edges. This oversegmented volume containing all supervoxels and the minimum spanning tree was ingested into Eyewire (https://eyewire.org) for crowdsourced proofreading.

Semiautomated reconstructions on Eyewire

Neurons were chosen for proofreading in Eyewire based on an initial set of ‘seed’ neurons that were identified as carrying eye position signals by co-registering the EM volume to calcium imaging performed on the same animal²². All pre- and postsynaptic partners of the initial seed of 22 neurons were reconstructed. Following this, we reconstructed partners of the neurons that were reconstructed in the initial round in a random manner. Eyewirers were provided the option of agglomerating (merging) supervoxels using a slider to change the threshold of agglomeration. To ensure accurate reconstructions, we did two things: (1) only players who met a certain threshold (see below), determined by their accuracy on a previously published retinal dataset^14,77, were allowed to reconstruct zebrafish neurons, and (2) the reconstructions were performed by two players in two rounds, in which the second player could modify the first player’s reconstruction (Supplementary Information). Finally, after two rounds of reconstruction, neuronal reconstructions were checked and if necessary corrected by expert in-house image analysts who each had more than 5,000 h of experience. The accuracy of the players in the crowd compared to experts (assuming experts are 100%) was >80% in the first round and ~95% after the second round of tracing. The validated reconstructions were subsequently skeletonized for analysis purposes. Player accuracy was calculated as an F1 score, where F1 = 2TP/(2TP + FP + FN), where TP represents true positives, FP represents false positives, and FN represents false negatives. All scores were calculated as a sum over voxels. TP was assigned when both the player and the expert agreed that the segmentation was correct, FN was assigned when the player missed segments that were added in by the expert, and FP was assigned when the player erroneously added segments that did not belong. Two F1 scores were calculated for each player, once for round 1 and once for round 2. No player played the same neuron in both rounds. Typically, at an agglomeration threshold of 0.3, the segmentation had an F1 score of 62%.

Only the most experienced players on Eyewire were allowed to participate. A small group of four highly experienced players received an invitation to test this new dataset. The players were given the title of ‘Mystic’, which was a new status created to enable gameplay and became the highest achievable rank in the game. Subsequent Mystic players had to apply for the status to unlock access to the zebrafish dataset within Eyewire. There was a high threshold of achievement required for a player to gain Mystic status. Each player was required to reach the previous highest status within the game as well as complete 200+ cubes a month and maintain 95% accuracy when resolving cell errors. Once a player was approved by the lab, they were granted access to the zebrafish dataset and given the option to have a live tutorial session with an Eyewire Admin. There was also a prerecorded tutorial video and written tutorial materials for players who could not attend the live session or who desired a review of the materials. Newly promoted players were also given a special badge, a new chat color and access to a new chat room exclusive to Mystics. These rewards helped motivate players by showing their elevated status within the game as well as giving them a space to discuss issues specific to the zebrafish dataset.

Cells were parceled out in batches to players. When a cell went live on Eyewire, it could be claimed by any Mystic. Each cell was reconstructed by only one player at a time. Once this player had finished their reconstruction, a second player would check over the cell for errors. After the second check, a final check was done by an Eyewire Admin. To mitigate confusion when claiming cells, a special graphical user interface was built into the game that allowed players to see the status of each cell currently online. A cell could be at one of the following five statuses: ‘Need Player A’, ‘Player A’, ‘Need Player B’, ‘Player B’ and ‘Need Admin’. These statuses indicated whether a cell needed to be checked or was in the process of being checked and whether it needed a first-, second- or Admin-level check. At each stage, the username of the player or Admin who had done a first, second or final check was also visible. It was made mandatory that the first and second checks were performed by two separate players.

Collaboration and feedback were important parts of the checking process. If a player was unsure about an area of the cell they were working on, they could leave a note with a screenshot and detail of the issue or create an alert that would notify an Admin. If a ‘Player B’ or an Admin noticed a mistake made earlier in the pipeline, they could inform the player of the issue via a ‘Review’ document or through an in-game notification (player tagging).

To differentiate the zebrafish cells from the regular dataset, each cell was labeled with a Mystic tag. This tag helped identify the cells as separate from the e2198 retinal Eyewire dataset and also populated them to a menu of active zebrafish cells within Eyewire.

Players were rewarded for their work in the zebrafish dataset with points. For every edit they made to a cell, they received 300 points. Points earned while playing zebrafish were added to a player’s overall points score for all gameplay done on Eyewire and appeared in the Eyewire leaderboard.

Skeletonization

The neuron segmentation IDs were ingested to an AWS SQS queue, and multiple distributed workers were launched in Google Cloud using kubernetes. Each worker fetched the segmentation chunks associated with a neuron ID. The segmentation voxels were extracted as a point cloud, and the distance to boundary field (DBF) was computed inside each chunk. Finally, a modified version of the skeletonization algorithm TEASAR was applied⁷⁸. Briefly, we constructed a weighted undirected graph from the point cloud, where the neighboring points are connected with an edge and the edge weight is computed from the DBF. We then took the point with the largest DBF as source and found the furthest point as the target. The shortest path from source to target in the graph was computed as the skeleton nodes. The surrounding points were labeled as visited, and the closest remaining unvisited point was taken as the new source. We repeated this process until all the points were visited. The skeleton node diameter was set as its DBF. The skeleton nodes were postprocessed by removing redundant nodes, removing ‘hairs’ based on diameter, removing branches inside somata, downsampling the nodes, merging single-child segments and smoothing the skeleton path. All skeletonization was performed at multum in parvo level 4.

Synapse detection

Synapses were automatically segmented in this dataset using neural networks to detect clefts and assign the correct partner as previously described³⁰. Briefly, a subset of the imaged data (219 μm³) was selected for annotation. The annotations were performed using the manual annotation tool VAST⁶⁷. Trained human annotators labeled the voxels that were part of the postsynaptic density and presynaptic docked vesicle pools. A convolutional neural network³⁰ was trained to match the postsynaptic density, using 107 μm³ as a training set and 36 μm³ as a validation set and leaving the remaining 76 μm³ as an initial test set. All of these sets were compared to the predictions of the model tuned to an F-score of 1.5 on the validation set to bias toward recall, where recall = TP/(TP + FN). Biasing the predictor toward recall reduces false negatives at the cost of more false positives, which are easier to correct. Apparent human errors were corrected, and training was restarted with a new model. We also later expanded the test set by proofreading similar automated results applied to new sections of the datasets (to increase representation of rare structures in the full image volume). The final model used an RS-U-Net architecture⁷³ implemented using PyTorch⁷⁵ and was trained using a manual learning rate schedule, decreasing the rate by a factor of 10 when the smoothed validation error converged. The final network reached 86% precision and 83% recall on the test set after 230,000 training iterations.

A convolutional network was also trained to assign synaptic partners to each predicted cleft as previously described³⁰. All 361 synapses in the ground truth were labeled with their synaptic partners, and the partner network used 204 synapses as a training set, 73 as a validation set and the remaining 84 as a test set. The final network was 95% accurate in assigning the correct partners of the test set after 380,000 training iterations.

The final cleft network was applied across the entire image volume and formed discrete predictions of synaptic clefts by running a distributed version of connected components. Each cleft was assigned synaptic partners by applying the partner network to each predicted cleft within nonoverlapping regions of the dataset (1,024 × 1,024 × 1,792 voxels each). In the case where a cleft spanned multiple regions, the assignment within the region that contained most of that cleft was accepted, and the others were discarded. Cleft regions whose centroid coordinates were within 1 μm and were assigned the same synaptic partners were merged together to merge artificially split components.

Finally, spurious synapse assignments (that is, postsynapses on axons and presynapses on dendrites) were cleaned by querying the identity of the ten nearest synapses to every synapse, where each synapse was associated with its closest skeleton node on both the pre- and postsynaptic sides. If the majority of the ten nearest neighbors were of the same identity (presynaptic or postsynaptic), then the synapse was assigned correctly. If the majority were of an opposing identity, these synapses were assigned incorrectly and were deleted. This process eliminated 1,975 falsely assigned synapses (~2% of the total).

Registration to reference atlas

Registration of the EM dataset to the Z-Brain reference atlas³¹ was performed in two stages. We created an intermediate EM stack from the low-resolution (270 nm per pixel) EM images of the entire larval brain tissue. This intermediate stack had the advantage of a similar field of view as the light microscopy reference volume while also being of the same imaging modality as the high-resolution EM stack. The low-resolution EM stack was registered to the reference brain (elavl3:H2b-RFP) by fitting an affine transform that maps the entire EM volume onto the light microscopy volume. To do this, we selected corresponding points such as neuronal clusters and fiber tracts using the tool BigWarp⁷⁹. These corresponding points were used to determine an affine transform using the MATLAB least squares solver (mldivide). Subsequently, the intermediate EM stack in the same reference frame as the Z-Brain atlas was used as the template to register the high-resolution EM stack. This was performed in a similar manner by selecting corresponding points and fitting an affine transform. This transform was used to map the reconstructed skeletons from high-resolution EM space to the reference atlas space.

Identification of ABD neurons

We identified ABD_M neurons (Fig. 1), which drive lateral movements of the ipsilateral eye, by their overlap with the Mnx transgenic line (Supplementary Fig. 3a, left). ABD_M axons exited R5 and R6 through the ABD (VIth) nerve (Fig. 1f, black box) as reported previously²².

Medial movements of the contralateral eye are driven by the medial rectus muscle, which is innervated by motor neurons in the contralateral oculomotor nucleus, which in turn are driven by internuclear neurons (ABD_I) in the ipsilateral ABD complex (Fig. 1f). ABD_I neurons were identified (Supplementary Fig. 3a, right) by their overlap with two nuclei in the Evx2 transgenic line that labels glutamatergic interneurons. The ABD_I neurons were just dorsal and caudal to the ABD_M neurons, and their axons crossed the midline⁸⁰.

Identification of Ve² neurons

We identified a class of Ve² neurons (Fig. 1h, dark brown) that received synapses from primary vestibular afferents. The latter were orphan axons in R4 identified as the vestibular branch of the vestibulocochlear nerve (VIIIth nerve) by comparison with the Isl2 line, which labels the major cranial nerves (Supplementary Fig. 3b, blue axons). We speculate that Ve² neurons are descending octavolateral neurons but withhold final annotation until functional confirmation is available³².

Identification of RS neurons

RS neurons were divided into large and small groups (Fig. 1h). Large RS neurons were the M, Mid2, MiM1, Mid3i and CaD neurons. Small RS neurons were RoV3, MiV1 and MiV2 cells. These were identified by their stereotypic locations⁸¹ and by comparison with the Z-Brain atlas (Supplementary Fig. 4).

Centrality-based division into the center and periphery

The division of the reconstructed wiring diagram into center and periphery is based on standard measures of ‘centrality’, which have been devised in network science⁸². We define the simplest measure, known as degree centrality, as the geometric mean of the in-degree and out-degree of a neuron (it is more common to choose one or the other). Another popular measure, known as eigenvector centrality or eigencentrality, is a neuron’s element in the eigenvector of the connection matrix N_ij (the number of synapses onto neuron i from neuron j) corresponding to the eigenvalue with maximal real part; this measure extends the simpler concept of degree centrality by weighing a neuron’s connections by its centrality (a neuron is more central to the network if it receives inputs from other high-centrality neurons). Mathematically, this defines the eigenvector problem ν_i = ΣN_ijν_j, where ν_i is the (input) centrality of neuron i. An analogous formula, but instead replacing N_ij by its transpose (thus, defining left rather than right eigenvectors), can be used to weight output connections by the (output) centrality of the neuron to which output is projected. The eigenvector elements can be chosen non-negative by the Perron–Frobenius theorem. It is standard to use either the left or right eigenvector, but we use both for our definition by computing the geometric mean of the left and right eigenvector elements. Degree centrality and eigencentrality are correlated but not perfectly (Supplementary Fig. 1c). For a visualization of the network based on eigencentrality, see Supplementary Fig. 1e.

We define the periphery as those cells with vanishing (<10⁻⁸) eigencentrality but nonzero degree centrality. All but 62 of these 2,344 neurons had strictly 0 eigencentrality. The remaining 540 recurrently connected neurons are defined as the ‘center’ of the graph. See below for the effects of varying the eigencentrality threshold for center–periphery division.

Graph clustering

We applied two graph clustering algorithms to divide the center into two supermodules and obtained similar results from each algorithm. The clustering from the Louvain algorithm is presented in the main text and that of the spectral algorithm in Extended Data Fig. 3. We further subdivided each supermodule into subclusters using an SBM, as described below.

Louvain clustering

Graph clustering was performed using the Louvain clustering algorithm⁸³ for identifying different ‘communities’ or ‘modules’ in an interconnected network by optimizing the ‘modularity’ of the network, where modularity measures the (weighted) density of connections within a module compared to between modules. Formally, the modularity measure maximized is Q_gen = ∑B_ijδ(c_i, c_j), where δ(c_i,c_j) equals 1 if neurons a and b are in the same module and 0 otherwise, where ({B}_{ij}=frac{1}{omega }({W}_{ij}-gamma frac{{s}_{i}{s}_{j}}{omega })+{mathrm{transpose}}[frac{1}{omega }({W}_{ij}-gamma frac{{s}_{i}{s}_{j}}{omega })]). Here, s_i = ∑_cW_ic is the sum of weights into neuron i, s_j = ∑_bW_jb is the sum of weights out of neuron j, ω = ∑_cdW_cd is the total sum of weights in the network, and the resolution parameter γ determines how much the naively expected weight of connections (gamma frac{{s}_{i}{s}_{j}}{omega }) is subtracted from the connectivity matrix. Potential degeneracy in graph clustering was addressed by computing the consensus of the clustering similar to Sporns and Betzel⁸⁴. Briefly, an association matrix, counting the number of times a neuron is assigned to a given module, was constructed by running the Louvain algorithm 200 times. Next, a randomized association matrix was constructed by permuting the module assignment for each neuron. Reclustering the thresholded association matrix, where threshold was the maximum element of the randomized association matrix, provided consensus modules. We used the community_louvain.m function from the Brain Connectivity Toolbox package (https://sites.google.com/site/bctnet/home). In addition to the Louvain graph clustering algorithm, we also clustered the ‘center’ with an alternative graph clustering algorithm, spectral clustering, described below.

Spectral clustering

We used a generalized spectral clustering algorithm for weighted directed graphs to bisect the zebrafish ‘center’ subgraph, as proposed by Chung³⁹. Given a graph G(V, E) and its weighted adjacency matrix (Ain {{mathbb{R}}}_{ge 0}^{ntimes n}), where A_ij indicates the number of synapses from neuron i to neuron j, one can construct a Markov chain on the graph with a transition matrix P_α, such that ({[{P}_{alpha }]}_{ij}:= (1-alpha )cdot {A}_{ij}/{sum }_{k}{A}_{ik}+alpha /n). The coefficient α > 0 ensures that the constructed Markov chain is irreducible, and the Perron–Frobenius theorem guarantees that P_α has a unique positive left eigenvector π with eigenvalue 1, where π is also called the stationary distribution. The normalized symmetric Laplacian of the Markov chain is ({mathcal{L}}=I-frac{1}{2}left({Pi }^{1/2}{P}_{alpha }{Pi }^{-1/2}+{Pi }^{-1/2}{P}_{alpha }^{top }{Pi }^{1/2}right)).

To approximately search for the optimal cut, we use the Cheeger inequality for a directed graph³⁹ that bridges the spectral gap of ({mathcal{L}}) and the Cheeger constant ϕ^*. As shown in Gleich⁸⁵, the eigenvector v corresponding to the second smallest eigenvalue of ({mathcal{L}}), λ₂, results in optimal clusters. We obtained two clusters by a binary rounding scheme, that is, S₊ = {i ∈ V ∣ v_i ≥ 0} and S₋ = {i ∈ V ∣ v_i < 0}.

We modified the directed_laplacian_matrix function in the NetworkX package (https://networkx.github.io) to calculate the symmetric Laplacian for sparse connectivity matrices, with a default α = 0.05. The spectral gap for the eigenvector centrality subgraph is ({lambda }_{2}^{{mathrm{eigen}}}=0.137) and for the partitioned oculomotor (modO) module is ({lambda }_{2}^{{mathrm{eigen}}_{{mathrm{OM}}}}=0.256).

Degree-corrected SBM

Unlike the Louvain and spectral clustering algorithms that assume fewer intercluster connections than intracluster connections, SBMs assume only that there exist blocks such that the probability of two neurons being connected depends only on their block identities and degrees. SBMs are therefore capable of finding structures like cycles that Louvain clustering would not find because SBMs are built on intercluster connections. Starting with the two modules found by applying Louvain clustering to the ‘center’ subgraph, we applied an efficient statistical inference algorithm⁸⁶ to obtain SBMs for each module.

The traditional SBM⁸⁷ is composed of n vertices divided into B blocks with (left{{n}_{r}right}) vertices in each block and with probability p_rs that an edge exists from block r to block s. Here, we use an equivalent definition that uses average edge counts from the observation e_rs = n_rn_sp_rs to replace the probability parameters, and we construct a degree-corrected stochastic block model⁸⁸ that further specifies the in- and out-degree sequences (left{{k}_{i}^{+},{k}_{i}^{-}right}) of the graph as additional parameters.

To infer the best block membership (left{{b}_{i}right}) of the vertices in the observed graph G, we maximize the likelihood ({mathcal{P}}left(G| left{{b}_{i}right}right)=1/Omega left(left{{e}_{rs}right},left{{n}_{r}right},left{{k}_{i}^{+},{k}_{i}^{-}right}right)), where (Omega left(left{{e}_{rs}right},left{{n}_{r}right},left{{k}_{i}^{+},{k}_{i}^{-}right}right)) is the total number of different graph realizations with the same degree distribution (left{{k}_{i}^{+},{k}_{i}^{-}right}) and with (left{{e}_{rs}right}) edges among and within blocks of sizes (left{{n}_{r}right}), corresponding to the block membership (left{{b}_{i}right}). Therefore, maximizing likelihood is equivalent to minimizing the microcanonical entropy⁸⁹ ({mathcal{S}}left(left{{e}_{rs}right},left{{n}_{r}right}right)=ln Omega left(left{{e}_{rs}right},left{{n}_{r}right}right)), which can be calculated as ({mathcal{S}}simeq -M-{sum }_{i}left({k}_{i}^{+}!right)-{sum }_{i}left({k}_{i}^{-}!right)-{sum }_{rs}{e}_{rs}ln left(frac{{e}_{rs}}{{sum }_{s}{e}_{rs}{sum }_{r}{e}_{rs}}right)), where M = ∑_rse_rs is the total number of edges. We used the minimize_blockmodel_dl function in the graph-tool package (https://graph-tool.skewed.de) to bisect the central subgraphs by setting B_min = B_max = 2 and degcorr = true.

Shuffled networks

To test the degree to which network properties were determined by specific connections as opposed to statistical connections between blocks, we shuffled synapses while preserving a given block organization. For each cell, we initialized counters to the values of its blockwise in-degree and out-degree. We then randomly reassigned synapses in the following manner to shuffle connections while preserving these degrees. We picked a random presynaptic cell i and a random postsynaptic cell j under the constraint that the counter for the out-degree of cell i to the block containing cell j was greater than 0 and the counter for the in-degree of cell j from the block containing cell i was greater than 0. Each of these counters was then decremented by 1, and the process was repeated until all synapses were reassigned. In this way, once a cell had been selected enough times to reach its original in-degree and out-degree, it could no longer be chosen when assigning the remaining synapses. The shuffling procedure continued until all synapses were reassigned and the blockwise in- and out-degree of each cell was exactly preserved; if this became impossible midshuffle, the procedure was restarted. We considered three different organizations of modO into one, two and seven blocks and calculated each cell’s relative eye position sensitivity and best-fit double exponential decay dynamics as well as the variance explained by the leading eigenvectors and the eigenvalue distribution of the network for 100 random shuffles under each block organization (Extended Data Figs. 8 and 9).

Potential synapse formalism

We define a potential synapse as a presynapse–postsynapse pair within a certain threshold distance (Fig. 2d). This definition is somewhat different from the light microscopic approach, which defines a potential synapse^37,90 as an approach of an axon and dendrite within some threshold distance. Also, we use neurons reconstructed from a single animal, whereas the light microscopic approach aggregates neurons from multiple animals or ‘clones’ a single neuron many times⁹¹.

Calcium imaging and eye position signals

The complete methods for recording calcium activity used to create the functional maps are reported in Ramirez and Aksay⁵⁰. Briefly, we used two-photon, raster-scanning microscopy to image calcium activity from single neurons throughout the hindbrain of 7- to 8-day-old transgenic larvae (sex indeterminate) expressing nuclear-localized GCaMP6f (Tg(HuC:GCaMP6f-H2B) strain cy73-431 from the laboratory of M. Ahrens, HHMI Janelia Research Campus). Horizontal eye movements were recorded simultaneously with calcium signals using a substage CMOS camera. We used CalmAn-MATLAB software to extract the neuronal locations from fluorescence movies⁹².

We analyzed STA activity to determine which neurons were related to eye movements⁵⁰. For each cell, we interpolated fluorescence activity that occurred within 5 s before or after saccades to a grid of equally spaced, 0.33-s time points and then averaged the interpolated activity across saccades to compute the STA. Separate STAs were taken for saccades toward the left and right. We performed a one-way analysis of variance (ANOVA) on each STA to determine which neurons had significant saccade-triggered changes in average activity (P < 0.01 using the Holm–Bonferroni method to correct for multiple comparisons). To determine which of these neurons had activity related to eye position and eye velocity, we first performed a principal components analysis on the STAs from neurons with significant saccade-triggered changes. We found that the first and second principal components had postsaccadic activity largely related to eye movement and eye velocity sensitivity, respectively (see Fig. 3a in Ramirez and Aksay⁵⁰). We characterized each STA using a scalar index, named ϕ in Ramirez and Aksay⁵⁰, created from that STA’s projections onto the first two principal components. We found that this index provides a good characterization of the average eye position- and eye velocity-related activity seen across the population (see Fig. 3c in Ramirez and Aksay⁵⁰ for a map of values and population average STAs). Eye position and eye velocity neurons were defined as neurons with an STA whose value of ϕ was within a specific range (–83 to 37 and 38 to 68, respectively). We removed any neurons with presaccadic activity that was significantly correlated with time until the upcoming saccade. The locations of each neuron were then registered to the Z-Brain atlas³¹ (see Ramirez and Aksay⁵⁰ for complete details).

Categorization of functional cells into cell type was guided by registration to the EM dataset. Candidate functional ABD neurons were identified by proximity (6 μm) to any ABD neuron from the registered EM dataset. Functional Ve² neurons were identified by proximity (6 μm) to any Ve² neuron from the registered EM dataset; because the above restrictions filtered out all of the candidate Ve² neurons, which had very weak sensitivity to spontaneous eye movements, in this case we simply used the constraint that these neurons be deemed active in the CaImAn-MATLAB step. Candidate VPNI cells were determined to be the remaining cells in R4 to R7/8 that satisfied the above restrictions and were more than 30 μm away from the center of the abducens.

Relationship between firing rate and eye position

To assess the functional characteristics of various oculomotor neurons (Fig. 5), we fit a traditional model of eye position sensitivity to neuronal firing rates extracted from our fluorescence measurements. Neuronal firing rates were estimated, up to an unknown scaling factor, by deconvolving the raw calcium fluorescence traces using the deconvolution algorithm with non-negativity constraint described in Pnevmatikakis et al.⁹³. Comparison of the resulting relative firing rates across neurons in different populations was justified as we observed similar sensor expression levels and baseline noise levels in these populations.

We modeled the dependence of firing rate on eye position using the equation (r={[tilde{k}(E-{E}_{{mathrm{th}}})]}_{+}), where (tilde{k}) is the relative eye position sensitivity, E_th is the threshold eye position at which r becomes positive, and the function [x]₊ = x if x > 0 and 0 otherwise⁴⁹. To facilitate comparison of results across animals, we normalized the units of eye position before fitting the model by subtracting the median eye position about the null position (measured as the average raw eye position) and then dividing by the 95th percentile of the resulting positions. Because our focus was on a cell’s position dependence, we also eliminated the eye velocity-dependent burst of spiking activity at the time of the saccade that ABD and VPNI neurons are known to display by removing samples that occur within 1.5 s before or 2 s after each saccade. Saccade times were found in an automated fashion by determining when eye velocity crossed a threshold value⁵⁰. Finally, because the eye position and fluorescence were recorded at different sampling rates, we linearly interpolated the values of neuronal activity at the eye position sample times.

To fit the value of (tilde{k}), for each cell, we defined the eye movements toward the cell’s responsive direction as positive so that (tilde{k}) is positive by construction. We then determined the threshold E_th using an iterative estimation technique based on a Taylor series approximation of [x]+ described by Muggeo⁹⁴. Using the resulting estimate of E_th, we determined (tilde{k}) as the slope resulting from a linear regression (with offset) to r using E as a regressor. Because we do not know the cell’s responsive direction or preferred eye a priori, we ran the model four times (for each eye, once with movements to the left as positive and once with movements to the right as positive) and used the value of (tilde{k}) that resulted in the highest R² value.

As a goodness-of-fit measure, we required all neurons, except Ve² neurons, to have an R² value greater than 0.4. Additionally, non-Ve² neurons were required to have an STA with at least one significant time point (P < 0.01 by ANOVA using Holm–Bonferroni correction) as defined in Ramirez and Aksay⁵⁰ and to have a ΔF/F response that was loosely related to eye position (R² greater than 0.2 when we run the above model replacing r with ΔF/F). The relative eye position sensitivity, (tilde{k}), for fluorescence data was then scaled to the average physiological VPNI response from goldfish⁴⁹.

All functional neurons associated with the circuit schematized in Fig. 5a were ipsiversive in position sensitivity. All ABD neurons increased activity with ipsiversive steps in eye position. The vast majority of putatutive VPNI neurons (98%) also had ipsiversive sensitivity; those few cells with contraversive sensitivity were deemed unlikely to be part of the VPNI based on previous work^49,56 and not considered further. Candidate Ve² neurons were mixed in their sensitivity to the direction of eye movement (52% ipsiversive); both types were included in the distributions of Fig. 5d. However, based on previous work³² demonstrating contrasting activity patterns for cells with ipsilateral versus contralateral projections, it was assumed in the below model that only those with ipsiversive sensitivity had ipsilateral projections as schematized in Fig. 5a.

Identification of excitatory versus inhibitory neurons

Prior work has identified two major classes of VPNI cells, those with ipsilateral recurrent excitatory projections and those with inhibitory contralateral projections^21,49. In R7/R8, the former were found to have somata primarily within a medial glutamatergic parasagittal stripe associated with the Alx transcription factor and the latter with a more lateral GABAergic parasagittal stripe associated with the Abx1b transcription factor^21,95,96. We therefore reasoned that membership in modO, which was predicated to have an ipsilateral recurrent connection with another member of modO, selected for glutamatergic VPNI cells and selected against GABAergic VPNI cells (which were retained in the ‘periphery’). Consistent with this, the VPNI neurons found in the center were located primarily in a medial stripe running from R4 to R7/R8 (Fig. 2c) that overlapped in the Z-Brain atlas with a region of alx expression (ZBB-alx-gal4). ModO neurons at the extreme lateral edge of R5/R6, identified as Ve² neurons (see above), also had ipsilateral projections, but these have been identified previously as being inhibitory through structure/function analysis³².

Network model based on synaptic wiring diagram

A unilateral model of the oculomotor integrator was built using the reconstructed synapses for ABD, Ve² and generic modO neurons that contain the majority of the VPNI population. Although the VPNI is a bilateral circuit, previous experiments^20,56 have shown that one-half of the VPNI is nevertheless capable of maintaining the ipsilateral range of eye positions after the contralateral half of the VPNI is silenced. This may reflect that most neurons in the contralateral half are below a threshold for transmitting synaptic currents to the opposite side when the eyes are at ipsilateral positions⁴³. Therefore, we built a recurrent network model of one-half of the VPNI circuit based on the modO neurons that we had reconstructed from one side of the zebrafish brainstem. We did not include modA neurons, assuming that input from modA cells fell below a threshold needed to drive modO neurons, similar to the manner in which bilateral interactions have been shown to be negligible for the maintenance of persistent activity^20,43. We added the ABD neurons and the feedforward connections from modO to ABD to the model because the ABD neurons are the ‘read-out’ of the oculomotor signals in the VPNI. Projections from the Ve² population were taken to be inhibitory, and all other connections were taken to be excitatory, as explained above. The remaining neurons in modO were included as part of the VPNI; we did not consider other vestibular populations because only Ve² neurons in modO received vestibular afferents from the VIIIth nerve. Saccadic burst neurons and recently discovered presaccadic ramp neurons located in R2/R3 (ref. ⁵⁰) were outside of our reconstructed volume and were therefore not included. Candidate burst neurons in dorsal regions of R5 and R6 have also been recently identified⁹⁷; to examine the possible impact of misclassifying putative burst neurons as VPNI cells, we ran the model with and without these candidates (identified via registration to the functional maps in Ramirez and Aksay⁵⁰).

Directed connection weights between each pair of neurons were set in proportion to the number of synapses from the presynaptic neuron onto the postsynaptic neuron divided by the total number of synapses onto the postsynaptic neuron, ({W}_{ij}=pm beta frac{{N}_{ij}}{{Sigma }_{k}{N}_{ik}}). Thus, we assume that each element W_ij corresponds to the fraction of total inputs to neuron i that are provided by neuron j. We then constructed a linear rate model for the network, governed by (tau frac{d{r}_{i}}{dt}=-{r}_{i}+{W}_{ij}{r}_{j}), where r_i is the firing rate of the ith neuron, W_ij are the connection weights, and τ is an intrinsic cellular time constant. τ for ABD and Ve² neurons was fixed at 100 ms. The scale factor β and the intrinsic time constant τ for the remaining putative VPNI neurons then provided two free parameters that could be used to set the timescale of persistence for the leading two eigenvectors of the network. For a given choice of scale factor and VPNI neuron time constant, we simulated the response of the network to a random pulse of excitatory input and compared the time course of the leading principal components of the simulated network to that of the calcium imaging data. These parameters were tuned so that the simulations roughly matched the decay times of the leading two principal components in the data, resulting in an intrinsic VPNI neuron time constant of 1 s and a scale factor set such that the leading eigenvalue of the network was equal to 0.9. These free parameters of the network model were not finely tuned, and the precise values used are not critical to the results obtained here.

Relative eye position sensitivities were determined numerically by initializing all neurons to zero firing rate and then simulating the response of the network to a series of three saccades occurring at intervals of 7 s. The input received by the network during a saccade was modeled as a 10-ms pulse along a vector composed of a fixed component that was an equal mixture of the leading three eigenvectors of the weight matrix and a random excitatory vector with an amplitude that was 15% of the amplitude of the fixed component. The random component was assigned at the beginning of the simulation, so the network received the same input for each saccade. The same method used to relate firing rates extracted from calcium imaging data to position sensitivity was used for the simulated firing rates, with the exception that the threshold estimation step was not required for the simulations because all firing rates in the simulations were above threshold. Saccade times in the simulations were taken to be at the onset of each input pulse. Finally, to obtain absolute position sensitivities that could be compared to experiments, we multiplied the relative sensitivities by a single global scale factor that was determined by matching the average VPNI population responses from the model to the average physiological VPNI responses from goldfish⁴⁹.

For both the simulated network and the calcium imaging data, we fit each neuron’s firing rate during the period between 2 s and 6 s following a saccade to a double exponential function, (r(t)={a}_{1}{e}^{-t/{tau }_{1}}+{a}_{2}{e}^{-t/{tau }_{2}}), where the time constants were fixed at 10 s and 4 s, respectively, leaving the amplitudes of each exponential as the only free parameters. These time constants were chosen because a simulated network with leading eigenvectors having these time constants had principal components of its neuronal firing rates that consisted of mixtures of exponentials whose summed time courses approximately matched those of the leading two principal components of the data. We found that the correlation between these two amplitudes in simulation better matched the correlation seen in the data when the saccadic input consisted of fixed and random components, as described above. The exact number of leading eigenvectors included in the fixed component is not important to achieve this tuning of the correlation between a₁ and a₂. We chose to use the leading three eigenvectors because the eigenvalues associated with them were clearly separated from the central disk of eigenvalues.

As a test of the robustness of our results to possible errors in connectome reconstruction, we generated a connectome that accounted for the estimated false-positive and false-negative rates of synapse detection by our connectome reconstruction procedure. We generated 100 models by randomly varying the identified synapses according to the estimated false-positive and false-negative rates and calculated the connection weights as described above. The eye position sensitivities with this synaptic detection jitter were reported as the average of these 100 models (Extended Data Fig. 7b). We also tested how robust our results were to the cutoff criterion for including neurons in the recurrently connected center by progressively increasing the minimum eigenvector centrality criterion for counting a neuron as belonging to the center as opposed to the periphery. We then plotted how the simulation model results changed as the number of center neurons was decreased and simultaneously reported the resulting number of generic (non-Ve²) modO neurons (Extended Data Fig. 7a). For each of these robustness tests, we also performed a singular value decomposition and double exponential fits on the simulated firing rates to compare to the functional imaging results (Extended Data Fig. 7c,d). To characterize the degradation in model performance when the actual connectome was replaced by connectomes generated by spatial proximity (potential connections), we reran the position sensitivity analysis using potential connectomes defined for connections within 5 μm (Fig. 5e).

Statistics and reproducibility

Here, we briefly summarize factors relevant for rigor and reproducibility that have been addressed in more detail elsewhere in the manuscript.

EM data were acquired from one reimaged animal (Fig. 1). No statistical method was used to predetermine sample size. Reconstructions were seeded by a group of 22 neurons that had previously been identified as VPNI cells through functional imaging²². Reconstructions were semiautomated and validated (and if necessary corrected) by in-house image analysis experts. Synapses were automatically segmented with a convolutional network that was 95% accurate when tested on ground truth data; an error correction step checking for preidentity/postidentity eliminated 2% of the total. During subsequent analysis of connectivity, whenever statistical tests were applied, distributions were assumed to be normal, but this was not formally tested. Randomization was used extensively in determination of modular organization. Investigators were not blinded during these analyses.

Fluorescence microscopy data were previously acquired from 20 animals⁵⁰. No statistical method was used to predetermine sample size. A one-way ANOVA (with multiple comparison correction; normality was assumed) on STA activity was used to identify activity of significance. Investigators were not blinded during these analyses.

Reporting summary

Further information on research design is available in the Nature Portfolio Reporting Summary linked to this article.