Blog Details

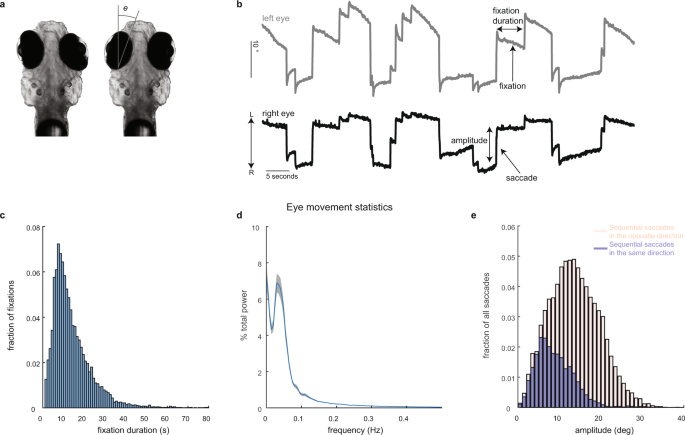
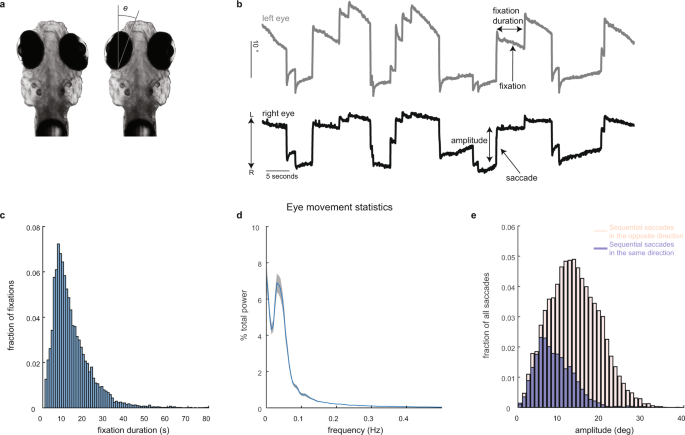
Calcium imaging and eye tracking

All experimental procedures were approved by Weill Cornell Medicine’s Institutional Animal Care and Use Committee. Transgenic larvae (7–8 days post fertilization) expressing nuclear-localized GCaMP6f, Tg(HuC:GCaMP6f-H2B; strain cy73–431), were kindly provided by Misha Ahrens’ lab. Fish were embedded in 1.5% low-temperature agarose and subsequently imaged using a custom-built two-photon laser scanning microscope (Daie, Goldman, and Aksay, 2015). We performed two-photon imaging using excitation light (930 nm) from a tunable laser (Spectra-Physics Mai Tai) sent through a 40× (0.8 NA) water-immersion objective lens (Olympus LUMPLFL40XW/IR2) to the hindbrain. The laser power was controlled using an electro-optical modulator (Conoptics 350-50UV) and amplifier (Conoptics 302RM). Laser power used for imaging ranged from 15–25 mW at the sample. Neurons within square horizontal planes (185 µm in length; 5–68 planes per fish spaced apart by 5 µm) were imaged simultaneously at 0.98 Hz (512 lines at 2 ms per line) by raster scanning implemented using ScanImage v3.5. Recordings lasted 4–5 min per plane. Images were saved as uncompressed grayscale TIFF stacks. Horizontal eye position (e in Fig. 1a) was extracted from camera images in real time at a variable sampling rate of ~13 Hz (refs. ^40,64), using a substage CMOS camera (Allied Vision Technologies, Guppy FireWire camera) illuminated with infrared light (850 nm, Thorlabs 851 L). The strong contrast in intensity between the zebrafish eyes and the surrounding, transparent, area on the head (Fig. 2a) was used to determine pixels covering the eyes. At the beginning of each experiment, the experimenter manually selected (using roipoly in MATLAB) a region-of-interest about which the eyes were free to move. Pixels within the region-of-interest whose intensity values were below a manually selected threshold were classified as belonging to the eyes. The threshold was chosen during the experiment by manually trying various values and selecting the one that achieved the best segmentation quality. After threshold, two ellipses were fit to the resulting binary image using the MATLAB regionprops function. Eye position equaled the orientation of the fitted ellipse about its time-averaged value.

Registration of individual planes to the Z-Brain atlas

Each imaging plane was first registered to a corresponding plane in a reference bridge brain constructed from a single Tg(HuC:H2B-GCaMP6f) fish (8 d.p.f.) using two-photon microscopy. Single planes in the bridge brain was constructed by stitching together six overlapping 512 × 512 (185 × 185 µm² area) images through an optimized translation procedure using the FIJI Grid/Collection Stitching Plugin^65,66. Each image used in the stitching procedure was formed by averaging calcium activity over a 20 s interval. The six images used were sufficient to completely tile any horizontal plane in the hindbrain. Bridge brain images were taken from across the entire extent of the hindbrain at a dorsal–ventral spacing of 3 µm. For each animal, we computed an affine transformation to linearly transform three-dimensional (3D) points from that animal to 3D points in the bridge brain. We used the BigWarp tool⁶⁷ in FIJI to select k corresponding locations between the brain being registered and the bridge brain. Correspondence was determined by visual inspection based on features, such as fiber bundles, the midline, and ventricles (Supplementary Fig. 1a). We used the MATLAB “” operator to solve the affine transformation ({bf{y}}={bf{Tx}},{boldsymbol{+}},{{bf{T}}}_{{bf{0}}}{boldsymbol{otimes }}{bf{1}}) for the 3 × 3 matrix, ({bf{T}}), and the 3 × 1 translation vector ({{bf{T}}}_{{bf{0}}}), where ({bf{y}}) and ({bf{x}}) are the 3 × k matrices of points chosen from the bridge brain and brain being registered respectively, ({bf{1}}) is a k × 1 vector of all ones and ({boldsymbol{otimes }}) denotes the outer product. We repeated this procedure to find corresponding points and an associated transformation matrix between the bridge brain and the Elavl3-H2B brain (Elavl3 is another name for the HuC gene) available on the Z-Brain website.

Image pre-processing to correct for movement artifacts

We were able to correct for small drifts that occurred during imaging using a motion-correction procedure based on cross-correlation. We first calculated the median fluorescence intensity across time for each pixel in the movie and used the resulting image as a reference. Any frame in the movie that deviated from the reference image was considered to have a movement artifact which required correction. To register each movie frame to the reference, we used the MATLAB function dftregistration.m⁶⁸, which implements image registration via cross-correlation. The dftregistration algorithm estimates the peak in the two-dimensional cross-correlation between the reference image and movie frame being registered. Each movie frame is then translated by an amount determined from the peak location. For computational efficiency, the dftregistration algorithm works in Fourier space to calculate cross-correlations. We used MATLAB’s built-in fast Fourier transform software (fft2) to compute each frame’s two-dimensional discrete Fourier transform (DFT) and to compute the two-dimensional DFT of the reference frame.

Detecting samples corrupted by animal movement

The motion-correction algorithm described above returned a scalar metric for each movie frame that indicated how well the frame matched the reference after correction. If this value was too low, the frame was considered too aberrant to be useful and the fluorescence of all pixels in this frame were replaced by NaNs. Specifically, for each frame, the dftregistration algorithm returned an error value related to the square root of one minus peak, normalized cross-correlation between a given frame and the reference. For each imaging plane, we computed the median error across all frames and the median absolute deviation (MAD) of the error across all frames. If a given frame’s error value was greater than five times the MAD plus the median that frame’s pixels were replaced by NaNs.

Automated identification of active cells

We determined the locations of active cells by running the freely available CalmAn-MATLAB toolbox provided by the Flatiron Institute (https://github.com/flatironinstitute/CaImAn-MATLAB)³⁵ on motion-corrected fluorescence movies. The algorithm models a calcium fluorescence movie as the product of two nonnegative matrices, one containing spatial locations and the other containing calcium time series for each active cell, plus a background and noise component. To determine the nonnegative matrices that best-fit the data, we implemented a procedure based on the demo_script.m file provided with the code. After initializing the spatial and temporal components, we ran one iteration of spatial and temporal updates, followed by a post-processing step, where components correlated with each other were merged and components that were poorly correlated with the data were removed, followed by a final spatial and temporal update.

We first found initial estimates for the spatial, temporal, and background components, using the initialize_components function. This function ran several steps: (1) it spatially filtered the fluorescence movies (Gaussian kernel with standard deviation set to 5, which corresponds to 1.8 µm). (2) It greedily selected locations where the spatial estimates explained the largest amount of spatio-temporal variance. (3) It used rank 1, nonnegative matrix factorization to produce spatial, temporal, and background estimates. (4) It refined these estimates using a hierarchical, alternating, nonnegative matrix factorization method. (5) It ran a rank 1 nonnegative matrix factorization on the spatio-temporal residual to initialize the background spatial and temporal components.

We updated the initial estimates of the spatial footprints and the background component, using the constrained nonnegative Lasso algorithm implemented in the update_spatial_components function. We used the dilate option which restricted the search of possible nonzero component values to a dilated version of that component’s nonzero values found in the previous iteration (dilation was performed using a 4-pixel radius (1.4 µm) disk-shaped structuring element). The new components are then post-processed by the following operations: (i) two-dimensional median filtering with a default size of 3 × 3 pixels, (ii) morphological closing with a square-shaped structuring element (3 pixels long), and (iii) “energy” thresholding with threshold set to 0.99. We then updated the estimates of the temporal components using the update_temporal_components function with an auto-regressive parameter, p, equal to zero. This function updated components using a block-coordinate descent algorithm (we used two iterations) which, with p equal to zero, ran a thresholding operation (at a threshold of 0) on the activity of each component after removing the effect of all the other components. After one spatial and temporal update, we removed spatial or temporal components that were poorly correlated with the raw data (space and time r values returned by classify_comp_corr function were <0.05) or whose spatial footprint areas were smaller than a value of 16 pixels squared which equaled 2.1 µm². We then merged spatially overlapping components with highly correlated temporal activity (cc > 0.95), using the merge_components function.

Using the new component estimates, we then ran one more iteration of the spatial component update followed by one more iteration of update_temporal_components, however p was now set to one instead of zero. When p > 0, the temporal update deconvolves the activity of each component after removing the effect of all the other components. We used the default constrained_foopsi method along with the CVX toolbox for deconvolution, which solved a noise-constrained optimization problem to produce estimates of denoised fluorescence activity and nonnegative spike estimates. We estimated the noise level for each neuron by averaging the power spectral density of component fluorescence activity over high frequencies (one half the Nyquist frequency to the Nyquist frequency which equaled 0.24–0.49 Hz for our data). We set the auto-regressive parameter to a fixed value, equal to 1.3 s in the equivalent continuous time model, which we chose by measuring the rate of decay of putative VPNI cells when they transition from spiking to quiescence. Simultaneous electrophysiological and calcium recordings of VPNI cells from previously performed experiments have shown that such a procedure can be used to accurately estimate the auto-regressive parameter⁴⁰. VPNI cells were selected as cells in rhombomeres 5–8 whose Pearson correlation coefficient between fluorescence and eye position was reasonably high (>0.5). As an initial approximation of the effects of calcium buffering on the relationship between firing rate and eye position, we convolved the eye position using an exponential decay kernel with a 1-s decay time before measuring the correlation. We then fit a decaying exponential function ((A{e}^{-t/tau }+b)) to the average fluorescence triggered around nasally directed saccades made by the eye ipsilateral to the cell. (b) was chosen as the average value of the ipsiversive STA 1–2 s prior to saccade. (A) and (tau) were found by minimizing the squared error between the model and data using an interior-point algorithm (MATLAB fmincon) with (tau) constrained to be positive and (A) constrained to be larger than (b). We used the median value of (tau) from cells that were well fit by the exponential decay model (r² > 0.8), as the parameter for the auto-regressive model (we converted the value from seconds to the equivalent discrete-time model). We used the nonnegative, sparse deconvolved output from this temporal update as our estimate of deconvolved neural activity. We estimated each component’s noisy fluorescence activity as the trace that resulted after spatially averaging the fluorescence video using that component’s spatial values as weights.

We investigated different initial values of the number of neurons parameter, K, in function initialize_components, and chose a value (250) that produced reasonable looking spatial footprint estimates based on visual inspection of a handful of sample fluorescence movies. Footprints in our final dataset had a size of 14.9 ± 0.1 µm² (mean ± SEM; n = 62,896 cells examined over 20 fish), which aligned closely with the typical area of the nucleus visualized by H2B-GCaMP (Fig. 2a). We registered each cell to a reference brain (see “Methods” section “Registration of individual planes to the Z-Brain atlas”) and excluded cells that were registered to the midbrain.

Cell detection based on time-averaged intensity images

In the “Results” section (“Mapping activity using two-photon microscopy”), we give estimates of the total number of cells in our dataset, and in Supplementary Fig. 1d, e we refer to non-active cells that were not selected by the CalmAn algorithm. For these sections only, we analyzed time-averaged images to infer cell locations since the CaImAn algorithm cannot find non-active cells (non-active cells are included as part of a single background term).

For each motion-corrected fluorescence movie, we calculated the median intensity across time for each pixel and analyzed the resulting time-averaged image to find individual cell nuclei locations. We performed a morphological opening on the time-averaged image (MATLAB function imopen) with a disk-shaped structuring element that had a radius equal to 4 pixels (1.4 µm). The opening operation with this structuring element tended to make it easier to segregate the disk-shaped nuclei in the image. We then found local intensity maxima of the opened image by looking for connected pixels with equal intensity that were greater than the intensity of external boundary pixels (MATLAB function imregionalmax). We measured the locations of individual cell nuclei measuring the regions of connected pixels that corresponded to local intensity maxima. To control for false positives, we excluded any regions-of-interest that had an area greater than most cell nuclei areas, which we determined by manual measurements (18.7 µm² which translated to 144 pixels squared).

Automated determination of saccade times

We determined the times of saccade occurrence by calculating the crossing times of eye velocity past a threshold. To calculate eye velocity, we first filtered out fluctuations in eye position using a median filter (medfilt1 in MATLAB). The exact value of the filter order depended on the eye position sampling rate, but was chosen to correspond to 500 milliseconds. We then approximated eye velocity as the difference in filtered eye position at consecutive time points divided by the time difference between these points. The threshold was set to three standard deviations above the mean-absolute velocity or 10° s⁻¹, whichever was larger. A single saccadic event typically consisted of several consecutive points whose velocity was above the threshold. We took the initial point as the time when the saccade occurs. During head/body movements the eye position traces become corrupted. One signature we used to determine when head/body movements occur is the time between threshold-crossing events (this signature was used in combination with the criteria listed in “Methods” section “Detecting samples corrupted by animal movement”). Separate experiments with video recordings of the entire body suggested that unusually short intervals between events typically indicate that the events occur during sudden head/body movements. For this reason, we did not consider threshold-crossing events that were spaced apart in time 1.4 s or less to be saccades.

Saccade-triggered average calculation

We averaged saccade-triggered signals across fixations after linearly interpolating them to a grid of time points equally spaced apart by 1/3 s. Activity before and after each saccade was extracted, interpolated (using interp1 in MATLAB with the linear method), grouped across saccades and then averaged according to the direction of saccade (left or right; Fig. 2c–e). We performed this procedure using deconvolved fluorescence and dF/F, where dF/F was computed as raw fluorescence, (F), subtracted and divided by its mean across the entire recording period, ({F}_{0}), ({rm{d}}F/F=frac{F-{F}_{0}}{{F}_{0}}). We chose a window that extended 5 s before and after saccade because at this value we retained a reasonable amount of data, while still finding patterns with time across the STAs (Fig. 3g). We excluded any cells that were recorded during an experiment that contained less than five saccades to the left and five saccades to the right (ten saccade-triggered responses total). Each of the saccades were required to be preceded and followed by a fixation that lasted at least 5 s. Of the 62,896 cells in the hindbrain that were identified as active by CaImAn, 36,527 cells had at least five left and right saccade-triggered responses that lasted 5 s or longer. Based on visual inspection of activity, we removed cells whose fluorescence activity near saccade was in the lowest 1% (375 total) of peak absolute STA values (peak absolute levels <14% dF/F) leaving 36,152 cells for eye-movement analysis. A 95% confidence intervals about the average (Fig. 2c–e) were found by resampling the saccade-triggered dF/F responses with replacement and calculating the STA for each resample (number of resamples = 100). We measured the lower and upper bounds of the confidence intervals as the 0.025 and 0.975 quantiles across the bootstrapped samples.

Selection of eye-movement responsive cells

We ran a one-way ANOVA (MATLAB function anova1, Statistics and Machine Learning Toolbox) on saccade-triggered responses to test the null hypothesis that STA activity was equal at all time points versus the alternative that at least one time point had average activity that differed from the others. We considered a neuron as being eye-movement responsive if we rejected the null hypothesis for either one of that neuron’s two STAs (the STA triggered around saccades to the left or right). We used the Holm–Bonferroni method⁶⁹ to correct for multiple comparisons. This procedure varied the significance level for each comparison by the formula (frac{alpha }{N-j+1}), where (j) was the index of the comparison after sorting p values from low to high, (alpha) was the desired family-wise error rate, and (N) was the total number of comparisons. We set (alpha) to 0.01 and set the number of comparisons to 72,304 (36,152 active cells with STAs available for analysis times two to account for both saccade directions, see “Methods” section “Saccade-triggered average calculation”). We rejected the null hypothesis for 6,712 cells (19% of 36,152 active cells). The probability that a hindbrain cell is eye-movement responsive is therefore 0.05 (the probability that a given active hindbrain cell is eye-movement responsive, 0.19, times the probability that a hindbrain cell is active, 62,896/238,191).

Principal component analysis of saccade-triggered averages

We ran a PCA to search for lower-dimensional representations of STAs across the population of eye-movement responsive cells. We combined STAs of deconvolved fluorescence from all eye-movement responsive cells (across all planes and fish recorded) and from both directions (around saccades to the left and right) resulting in a matrix, ({bf{f}}), that had (N=13text{,}424) rows (6,712 cells times two directions) and (T=31) columns (time around the saccade is evaluated at 31 discrete-time bins of size 1/3 s). To focus our analysis on the variations in dynamics across cells, we divided each STA by its L2 norm before performing PCA,

for (i=1,ldots ,N), (t=1,ldots ,T.) PCA (computed using MATLAB’s Statistics and Machine Learning Toolbox function pca) applied to ({bf{f}}^{prime}) resulted in a matrix, ({bf{u}}), of 31 orthonormal basis vectors (each (T) elements long) which we refer to as components (Fig. 3b) and a matrix of coefficients, ({bf{c}}) ((N) × (T) elements; Fig. 3c), that scale ({bf{u}}) such that,

for (i=1,ldots ,N), (t=1,ldots ,T.)

To illustrate the main features of variation across the population of neurons recorded, we focused on the coefficients corresponding to the first three components after determining that these components explained the majority of the variance (Fig. 3a). In Fig. 3c, the coordinates ({c}_{i1}), ({c}_{i2}), and ({c}_{i3}) are plotted on the ({c}_{1})-axis, ({c}_{2})-axis, and ({c}_{3})-axis, respectively, for (i=1,ldots ,N). We normalized these coefficients to have unit norm,

for (i=1,ldots ,N), (j=1,2,3). We then transformed ({{bf{c}}}^{prime}) into spherical coordinates (see Fig. 3c).

for (i=1,ldots ,N). The elements ({Phi }_{i}) and ({Theta }_{i}) contain the ({i}{{rm{th}}}) STA’s values of the angles (phi) and (theta) shown in Fig. 3c and are used to construct Fig. 3c–h, and Supplementary Figs. 2 and 3. Note that we are working with latitude, which we have defined to be 0 at the equator in Fig. 3c, d, instead of the azimuthal angle ((90-theta)) typically used when working in spherical coordinates. The principal advantage of working in spherical coordinates is that we can examine two-dimensional plots without sacrificing the temporal information stored in the first three principal components. The phases of ({boldsymbol{Phi }}) and ({boldsymbol{Theta }}) were chosen so that the ({i}{{rm{th}}}) STA whose temporal profile is equal to components one, two, or three would have coefficients, (left({Phi }_{i},{Theta }_{i}right)), equal to (0°, 0°),(90°, 0°), (0°, 90°), respectively, as shown in Fig. 3c. The two-dimensional probability density function over ({boldsymbol{Phi }}) and ({boldsymbol{Theta }}) shown in Fig. 3d was measured using a normal Gaussian kernel smoothing function (MATLAB, Statistics and Machine Learning Toolbox function ksdensity with bandwidth parameter equal to 10° for ({boldsymbol{Phi }}) and 3° for ({boldsymbol{Theta }})).

Each population average shown in Fig. 3g is constructed by averaging together all non-normalized STAs triggered to saccades to the left with a specific value of (phi). For example, the average under the column (phi) = 105 was constructed by first finding the STAs triggered to saccades to the left with (phi) within 15° of 105 and then averaging these together. Letting ({{bf{f}}}_{i,:}) denote the ({i}{{rm{th}}}) STA and ({{mathcal{S}}}_{105}) denote the set of integers that index leftward STAs with (phi) = 105, ({{mathcal{S}}}_{105}=big{i|{97.5le Phi }_{i} ,<, 112.5,text{and}{{bf{f}}}_{{boldsymbol{i}},}:,text{is},, text{an},, text{average},, text{of},, text{responses},, text{triggered},, text{to},, text{leftward} ,,text{saccades}big}), the population average under the column (phi) = 105 is computed as

where (|{{mathcal{S}}}_{105}|) denotes the number of STAs indexed by the set ({{mathcal{S}}}_{105}). The population averages shown in Supplementary Fig. 3a are constructed in the same way except with the condition that STAs are triggered to saccades to the right. The population averages shown in blue in Fig. 3f are constructed in the same way except without the restriction on saccade direction. Note that the population averages shown in Fig. 3f, g and Supplementary Fig. 3a do not use the L2-normed responses, are constructed using all principal components and only use the angles in ({boldsymbol{Phi }}) to group STAs. Therefore, the population averages that are displayed can reflect variations not captured by the first three components.

K-means clustering of saccade-triggered averages

K-means was used to cluster the normalized coefficients (defined in Eq. (3) and associated text) found by PCA on STAs from eye-movement responsive cells (Supplementary Fig. 2). For each cell, we focused on the normalized coefficients that scale the first three principal components. We created a six-dimensional vector by combining the normalized coefficients that correspond to the STA triggered to saccades to the left and right. To choose the number of clusters, we ran nine K-means analyses, using a different number of clusters on each run (between 2 and 10) to group the combined coefficients, and we used the silhouette value to measure cluster quality. The silhouette value for an individual vector measures how close that vector is to other vectors in its own cluster relative to its distance with vectors in other clusters. The value for the ({i}{{rm{th}}}) vector is defined as the minimum average distance from the ({i}{{rm{th}}}) vector to all vectors in different clusters than the ({i}{{rm{th}}}) vector, b_i, minus the average distance from the ({i}{{rm{th}}}) vector to other vectors in the same cluster, a_i. The silhouette value is normalized by max(a_i , b_i) in order for it to range from +1 to −1 with vectors that are well matched to their cluster having values near +1, and with vectors that are randomly clustered having values near 0.

Anatomical projections

We created maps of SR cell locations (Fig. 6d, e) and of the angle (varphi) shown in Fig. 3c (computed as described in Eq. (6) and related text) from STAs triggered to saccades to the left (Fig. 3h)/right (Supplementary Fig. 3b) for each fish and imaging plane. Since some regions were imaged with more fish than others (Supplementary Fig. 1c), these maps were created using a randomly selected subset of the eye-movement responsive cells. To adjust for variation in the number of fish sampled across brain regions (all regions were sampled by at least three fish), we assigned each cell a probability of being included in the map equal to three divided by the number of fish sampled at that cell’s location. Each projection was made by first registering cell locations to the Z-Brain (see “Methods” section “Registration of individual planes to the Z-Brain atlas”) and then binning cells into 2D square bins (5 µm in length) appropriate for the given projection. The modes shown in Fig. 3h and Supplementary Fig. 3b were computed by first constructing a histogram (15° bins) of the values of (varphi) from STAs triggered to the left/right from cells registered to a given square in the projection. The color displayed was determined by the value where the histogram peaked or, in cases where the histogram had multiple modes, was determined by the value at a randomly chosen peak.

Selection of SR cells

An eye-movement responsive cell was classified as an SR cell if its dF/F response before upcoming saccades was significantly correlated with time before saccade. We measured two Spearman correlations for each eye-movement responsive cell. One correlation was computed (MATLAB, Statistics and Machine Learning Toolbox function corr with option type set to Spearman) on values of dF/F and time before saccade concatenated from all fixations before saccades to the left. The other correlation was computed on values of dF/F and time before saccade concatenated from all fixations before saccades to the right. The Spearman correlation can be used to measure monotonic (not only linear) relationships between two variables (X) and (Y). It is calculated as the standard Pearson correlation coefficient applied to the ranks of (X) and (Y). We did not interpolate fluorescence activity before computing the correlation coefficients. Since we were interested in cells whose activity is related to upcoming saccade, we did not include activity that was within 2 s of the previous saccade, where eye-movement responsive cells might have post-saccadic fluorescence decays. We computed a p value for each correlation by testing the hypothesis that rho = 0 against the alternative that the correlation was greater than 0 (tail option set to right). A neuron was considered to have significant pre-saccadic activity if we rejected the null hypothesis for any of the cell’s two correlation coefficients at a significance level of 0.01. To correct for multiple comparisons, we used the Holm–Bonferroni method (as described in “Methods” section “Selection of eye-movement responsive cells”) with the number of comparisons set to 13,424 (the number of eye-movement responsive cells times two directions).

Measuring SR cell activity rise time

We measured the time when an SR cell’s activity rose above baseline by determining when its deconvolved fluorescence crossed a threshold near zero (0.1). Based on the visual inspection of deconvolved SR traces, we found that the nonnegativity constraint used to compute deconvolved fluorescence facilitated the distinction between times when the cell was responsive from times when it was not (Fig. 4a). Epochs of time where the deconvolved estimate was equal to, or nearly equal to, zero were interpreted as epochs where the cell was not responsive. Therefore, we measured SR cell activity rise time for each fixation (Fig. 4b), as the time point before its deconvolved fluorescence increased >0.1.

Measuring rate of pre-saccadic rise in single SR cells

We estimated the rate of pre-saccadic rise in SR cells by finding the slope of the best-fit line of pre-saccadic deconvolved fluorescence with time. To construct the best-fit line we used time from pre-saccadic rise to the time of upcoming saccade as a regressor to a linear regression that fit deconvolved fluorescence values. The linear approximation was reasonable for 72% of the fixations (correlation between regression fit and data was >0.4). We excluded fixations where we were unable to measure the slope with linear regression.

Predicting saccade direction using choice probability

We predicted saccade direction using interpolated SR activity before saccadic events. Throughout this section, the phrase “interpolated SR activity” refers to linear interpolation of deconvolved fluorescence activity to a grid of equally spaced time points (using 1/3 s bins) starting from the previous saccade to the upcoming saccade.

The CP is a commonly used metric in neurophysiology and psychophysics experiments that quantifies how well an ideal observer can predict animal behavior³⁷. In a typical neurophysiology application, the CP measures relationships between neuronal discharges and binary behavioral choices. We adapted this metric by using the spontaneous decision to saccade to the left or the right as our binary behavioral variable, and population average deconvolved fluorescence at a given time before saccade as our neural read-out. At discrete time points before upcoming saccades, we made two histograms of interpolated SR activity. One distribution, referred to as the noise distribution, was comprised of values of interpolated SR activity before saccades to the right (left) from SR cells significantly correlated with upcoming saccades to the left (right). The other distribution, referred to as the signal distribution, was comprised of interpolated SR activity before saccades to the left (right) from SR cells significantly correlated with upcoming saccades to the left (right). Saccade direction was predicted using a threshold on population activity. We plotted the fraction of interpolated SR activity from the signal distribution that was above threshold (the true positive rate) versus the fraction of interpolated SR activity from the noise distribution that was above threshold (the false positive rate) across multiple threshold values. The CP was calculated as the area under the resulting curve, which would equal 0.5 if activity and upcoming saccade direction were not related. To estimate the variability in CP, we computed multiple CPs each conditioned on a different fixation duration (fixing durations to values 2–20 s) and then computed the CP SEM across fixation durations.

Predicting saccade times using a ramp-to-threshold model

We predicted when a saccade would occur by calculating a running estimate of population activity slope and then plugging this estimate into a ramp-to-threshold model to predict when population activity will cross a threshold, (kappa). We first measured (kappa) by averaging deconvolved fluorescence reached at the time of saccade across all SR cells in our dataset. For each fixation duration, we then calculated population average activity before upcoming saccade by combining (across all cells and fish) interpolated SR activity (Fig. 5e; we used eighteen nonoverlapping values of fixation duration from 3.5 ± 0.5 to 20.5 ± 0.5 s). We modeled the population average dynamics, (y(t)), at values of time (t) after population activity begins to rise, with the following linear ramp equation

where (D) is the population activity slope. After a time, ({t}_{r}), a saccade will occur and (y) should equal (kappa) if the ramp-to-threshold model is accurate, e.g.,

We constructed a running estimate of (D) by first measuring when the actual population activity, (widetilde{y}left(tright),) began to rise. Note that we are distinguishing the population activity measured from data, (widetilde{y}left(tright)), from the model of population activity, (y(t)), specified by Eq. (8). We measured when (widetilde{y}left(tright)) began to rise as the time when the derivative in (widetilde{y}left(tright)) crossed a threshold of 35 (arbitrary units). Note that under our convention we set this event to occur at time 0. The derivative was approximated as the difference between population activity at each time point divided by the interpolated time bin interval, (triangle t), of 1/3 s. We created a running estimate of (D) using the median value of the derivative from time 0 until time, (t),

We substituted our running estimate of the slope into Eq. (9) to yield a running estimate of ({t}_{r})

where we have used the ~ symbol to denote estimates of model parameters. Using our estimate (widetilde{{t}_{r}(t)}), we could predict the amount of time until upcoming saccade for any given value of (t), as (widetilde{{t}_{r}(t)}-t). Figure 5h shows predictions of the time until upcoming saccade made by varying the value of t from one time point after population activity begins to rise to one time point before saccade for each fixation duration.

In the text and in Supplementary Fig. 6, we also present results showing how well the population average activity is approximated by a ramp-to-threshold model. In these cases, we did not create a running estimate of the slope, but instead only created one slope estimate by setting ({t=t}_{r}) in Eq. (10). We used all cells to estimate (widetilde{Dleft(tright)}) when we forecasted saccade times for Fig. 5h, i; however, using all cells would have led to overfitting in Supplementary Fig. 6. To prevent overfitting in this case, we only used a random subset of all cells (60%) to measure (widetilde{y}left(tright)). We used this measurement to compute (widetilde{D}) (via Eq. (10) with ({t=t}_{r})) and then plugged (widetilde{D}) into Eq. (8) to predict population activity. We then tested this prediction against a new measurement of population activity constructed from the remaining 40% of cells. To determine model accuracy, we repeated this procedure on 10,000 randomly selected subsets from randomly chosen fixation durations.

Saccade time predictions by an ideal observer

As a control, we determined the fraction of saccades that could be accurately predicted given knowledge of the elapsed time since last saccade and the distribution of fixation durations. Given this information, an ideal observer could predict upcoming saccade times by guessing a time that minimizes some cost function that measures error between the actual saccade time and the guessed time. We tried three cost functions (mean-squared error, mean-absolute deviation, and all-or-none error) and report results in the text from the one that performed the best (all-or-none error).

Cluster laser ablations

We targeted regions along the dorsal–ventral axis that were 30 µm dorsal of the medial longitudinal fasciculus since this is where we found most eye-movement responsive cells. Ablations were performed with the same microscope used for imaging. Cluster ablations⁴⁰ were created by focusing the laser to an area smaller than a single cell and then increasing the average laser power to values between 130 and 150 mW for 1–5 s. We repeated this procedure until we saw a lesion, which we determined by looking for a multi-spectrum spot that was much brighter than the fluorescence of surrounding tissue. Lesion sizes with this procedure were generally ~5 µm in diameter. To increase the size of the lesion we lowered the average laser power to values of 30–50 mW and scanned the ablated region at these lower powers, which caused the lesion size to grow. We stopped scanning the ablated region once it grew to ~30 µm in diameter. We waited between 30 and 120 min after ablation before recording post-lesion eye movements.

To estimate the fraction of SR cells lesioned in a given fish during cluster ablations (Fig. 7d and text), we registered the ablated animals and SR cell locations to the bridge brain (see “Methods” section “Registration of individual planes to the Z-Brain atlas”) and then calculated the number, ({n}_{c}), of SR cells (locations shown in Fig. 6) that fell within a cylinder (30 µm radius, 60 µm side length along dorsal–ventral axis) centered about the location of peak ablation damage. To determine the cylinder center, we manually inspected time-averaged images of each the ablated region (Fig. 7a) to find planes containing a bright, multi-spectrum fluorescence characterizing ablation damage. We found the plane with the maximal damage, selected similar points between this plane and the bridge brain (as demonstrated in Supplementary Fig. 1a) and then created a 2D affine matrix to transform the center of the registered lesion to the bridge brain. The fraction ablated was equal to ({n}_{c}) divided by the total number of SR cells used to construct the map.

Single-cell laser ablations

In a separate set of experiments, we targeted individual SR neurons for ablation. We imaged neuronal activity in several planes (185 µm² in size) centered on regions most densely populated with SR cells (dorsal of the Mauthner cell between rhombomeres 2 and 6, see Fig. 6). During the experiment, we analyzed saccade-triggered activity of all cells in the imaging planes to identify the locations of eye-movement responsive cells (using the ANOVA based procedure described in “Methods” section “Selection of eye-movement responsive cells”) and then identified which of these cells were SR cells (using the procedure described in “Methods” section “Selection of SR cells”). The total time spent imaging and processing activity before ablation varied between 10 min and 2 h. After processing, we targeted four to seven randomly chosen SR cells for ablation. Before each ablation, we manually corrected for any changes in cell-center location that might have arisen during SR cell identification. Manual correction was performed by zooming into a region containing a cell of interest, taking a new time-averaged image, and reidentifying the SR neuron location by comparing the new with the original time-averaged image where the SR cell was identified. We did not attempt an ablation if the experimenter could not reidentify the cell of interest after processing. We ablated individual neurons by focusing a high-powered, pulsed femtosecond laser (810 nm, 400–500 mW after the objective) on the center of SR cells for a brief (2–5 ms) period of time^28,29,70. This procedure resulted in the loss of one to three cells per ablation attempt (Fig. 7b) at the depths where SR cells were targeted (40–70 µm below the surfaced). In some cases, ablations did not occur even after three to five attempts, most likely due to laser power absorption from pigmentation. We did not try to ablate a cell after attempts. In one experiment, we repeated three cycles of finding cells of interest in a single plane, ablating these cells, then searching for more cells of interest in subsequent planes. In all other experiments we imaged, identified cells of interest, and then ablated these cells. At the end of the experiment, we took time-averaged images of the entire hindbrain dorsal of the Mauthner cell and used this stack to register ablated cells to the Z-Brain Atlas. For control cell ablations, we performed the same procedure but targeted cells that failed to pass our criteria for being considered eye-movement responsive.

Analysis of behavior following laser ablations

For each fish, we measured fractional changes in median fixation duration after ablation. Since we were concerned with a spontaneous behavior, we could not control the number of fixations that were recorded during the timeframe of each experiment. As a result, our measurements would have had different accuracies per animal (Supplementary Table 1), if we calculated fractional changes without accounting for the different number of samples per fish. To control for this difference in accuracy, while using all our data, we made repeated measurements of the fractional change per fish with each repeated measurement computed using the same number of fixations before and after ablation. For each repeated measurement, we randomly sampled without replacement ({N}_{{{min }}}) fixations before and after ablation. The exact value of ({N}_{{{min }}}) was based on animals with the fewest number of fixations available after excluding animals that stopped making saccades after ablation; animals whose average saccade rate never increased above one saccade per direction per minute were excluded (n = 3 animals from cluster ablation experiments, 2 from treated group, and 1 from control). Specifically, if we denote the number of fixations before or after ablation (indexed by (i)) from animal (j), as ({n}_{{ij}}), then ({N}_{{{min }}}=mathop{{{min }}}nolimits_{i,j}{n}_{{ij}}). The number of times we repeated each measurement of fractional change in median fixation duration varied per fish and was determined by how many more fixations each animal made compared to ({N}_{{{min }}}). Specifically, the number of times we repeated each measurement for animal (j) equaled ({rm{round}},(frac{mathop{{{min }}}nolimits_{i}{n}_{{ij}}}{{N}_{{{min }}}})). The fractional change in median fixation duration was computed as the difference in median fixation duration (after minus before ablation) divided by the median fixation duration before ablation. Using (l) to denote the index of the repeated measurement in animal (j) and ({t}_{{ijml}}) to denote the ({m}{{mathrm{th}}}) randomly sampled fixation duration (integer ({m}) varies from 1 to ({N}_{{rm{min }}})) in condition (i) ((i)=1 denotes before ablation and (i) = 2 denotes after ablation), the fractional change in fixation duration was computed as:

for (l) = 1, 2, …, ({rm{round}}(frac{mathop{{{min }}}nolimits_{i}{n}_{{ij}}}{{N}_{{{min }}}})) and j = 1, 2, …, total number of animals.

To determine how the variability in cluster ablation results depended on the sample size used to compute the change in fixation duration, ({N}_{{{min }}}), we reran the entire procedure described >13 times each time setting a different floor to ({N}_{{{min }}}) (floor values equaled 55, 65, 75, …175). For each floor value, ({N}_{{{min }}}) was computed after removing every animal whose minimum value of fixations either before or after ablation was below the floor value (see minimum number of fixations per fish in Supplementary Table 2). At each floor value, we computed the Pearson correlation coefficient between the elements of ({bf{y}}) and the fraction of cells removed during a cluster ablation (see “Methods” section “Cluster laser ablations” for a description of how we estimated the fraction of SR cells ablated for each animal). Since the elements of ({bf{y}}) depend on the random samples chosen, we repeated our sampling procedure 100 times for each floor value to obtain 100 samples of ({bf{y}}), and subsequently 100 correlation coefficients and then computed the median across these samples resulting in 13 median correlation coefficients. In the “Results” section regarding cluster ablations (see “Focal laser ablations identify SR cells as indispensable for setting spontaneous fixation durations”), we presented the average correlation across these 13 values (({N}_{{{min }}}) varied between 57 and 176 fixations, n varied between 10 and 29 animals, see Supplementary Table 2 to determine exact n at a given floor). At each floor value, we also ran a one-sided, two-sample KS test between the 100 samples of correlation coefficients and 100 coefficients obtained by correlating randomly shuffled elements of ({bf{y}}), with the fraction of ablated SR cells. This resulted in 13 p values since we used 13 floor values. All 13 p values were significant at a criterion of 0.001 using the Holm–Bonferroni method to control for multiple comparisons. As expected, the variability in correlation coefficients increased when too few samples, ({N}_{{{min }}},) were used to compute each fractional change; the average correlation across the eight values with the largest values of ({N}_{{{min }}}) (({N}_{{{min }}}) varied between 105 and 176 fixations, n varied between 10 and 20 animals) = 0.33. The values plotted in Fig. 7d are from one of the hundred samples of ({bf{y}}) at ({N}_{{{min }}}) = 57 that contained a typical correlation coefficient; Supplementary Fig. 8d shows results from the same run used to construct Fig. 7d.

In the “Results” section regarding single-cell targeted ablations, we repeated our sampling procedure 100 times to calculate 100 samples of the mean of ({bf{y}}) and presented the minimum, maximum, and median across these samples. We did not remove animals for single-cell ablation analysis (({N}_{{{min }}}) = 33 fixations; see Supplementary Table 3 for the number of repeated measurements per animal (j), i.e., ({rm{round}}(frac{mathop{{{min }}}nolimits_{i}{n}_{{ij}}}{{N}_{{{min }}}})), where the conditions before and after ablation are indexed by (i)). Figure 7e shows one of the hundred runs of ({bf{y}}) that results in a typical change between SR and control-targeted groups. The sham ablation results presented in Fig. 7e were computed without making repeated measurements using ({N}_{{{min }}}) = 33 fixations per animal to compute fractional change in median fixation duration. For each sample of ({bf{y}}) for control and SR-targeted animals, we ran a Wilcoxon rank-sum test (100 tests in total) of the null hypothesis that the medians are equal between the distribution of ({bf{y}}) for SR-targeted and the distribution of ({bf{y}}) from control animals against the alternative that the median is greater in SR-targeted animals. The minimum, maximum, and median p values across the 100 runs were also presented in the results. MATLAB function ranksum with the appropriate value of tail was used to perform the one-sided Wilcoxon tests.

Reporting summary

Further information on research design is available in the Nature Research Reporting Summary linked to this article.